El ‘solitón’ de Peregrine observado por fin

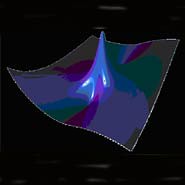
Una antigua solución matemática propuesta como prototipo para las famosas olas errantes oceánicas, responsables de muchas catástrofes marinas, se ha observado por primera vez en un sistema físico continuo.

El ‘solitón’ de Peregrine, descubierto hace 25 años por el fallecido Howell Peregrine (1938-2007), profesor de renombre internacional de Matemáticas Aplicadas anteriormente con sede en la Universidad de Bristol, es una solución localizada para una ecuación diferencial parcial compleja conocida como la ecuación de Schrödinger no lineal (NLSE).

La solución de Peregrine es de una gran relevancia física debido a que su intensa localización ha llevado a que se proponga como prototipo de olas errantes oceánicas y también representa un límite matemático especial de una amplia clase de soluciones periódicas a la NLSE.

Aunque a pesar de su lugar central como objeto definitorio de la ciencia no lineal durante unos 25 años, las características únicas de esta especial onda no lineal nunca se habían observado directamente en un sistema físico continuo – hasta ahora.

Un equipo internacional de investigación procedente de Francia, Irlanda, Australia y Finlandia informa de la primera observación de ondas altamente localizadas que poseen características casi ideales del solitón de Peregrine en la prestigiosa revista, Nature Physics.

Los investigadores llevaron a cabo sus experimentos usando luz en lugar de agua, pero fueron capaces de probar rigurosamente la predicción de Peregrine aprovechando la equivalencia matemática entre la propagación de ondas no lineales en el agua y la evolución de pulsos intensos de luz en fibras ópticas.

Basándose en décadas de desarrollo avanzado en fibra óptica e instrumentación óptica ultra-rápida, los investigadores fueron capaces de medir explícitamente las propiedades temporales ultra-rápidas de la onda solitón generada, y compararla cuidadosamente con los resultados de la predicción de Peregrine.

Sus resultados representan la primera medida directa de la localización del solitón de Peregrine en un entorno de ondas continuo en la física. De hecho, los autores tienen cuidado en resaltar que un solitón matemáticamente perfecto puede que nunca llegue a observarse en la práctica, pero también demuestran que su intensa localización aparece incluso bajo condiciones de excitación no ideales.

Este es un resultado especialmente importante para la comprensión de cómo las ondas errantes de alta intensidad pueden formarse en un entorno muy ruidoso e imperfecto como es el océano abierto.

Los hallazgos también destacan el importante papel que desempeñan los experimentos en óptica para clarificar las ideas de otros dominios de la ciencia. En particular, dado que la la dinámica relacionado gobernada por el mismo modelo de propagación NLSE también se observa en muchos otros sistemas como plasmas y Condensados Bose Einstein, se espera que los resultados estimules nuevas direcciones de investigación en muchos otros campos.

---

Artículo de referencia: http://dx.doi.org/10.1038/NPHYS1740.
Fecha Original: 22 de agosto de 2010
Enlace Original

La imposibilidad de imaginar números grandes o cosas grandes

Nuestro cerebro no está diseñado para imaginar números demasiado grandes, ni tampoco espacios u objetos de dimensiones gigantescas (o liliputienses), porque simplemente nuestros antepasados nunca tuvieron que preocuparse de cosas así. Bastaba con poder contar a los miembros del clan o del clan enemigo, por ejemplo.

Pero no tuvieron que enfrentarse nunca al tamaño del universo, o al número inabarcable de estrellas.

De modo que el único atajo que tenemos para enfrentarnos a conceptos semejantes es el uso de analogías que nos permitan establecer formas de visualizar las cosas de un modo diferente a la experiencia habitual.

Siempre digo, por ejemplo, que empecé a asimilar mínimamente el tamaño descomunal del Universo cuando leí la novela de ciencia ficción Tau Cero, de Poul Anderson, en la que se narra de forma convincente los efectos de la dilatación temporal einsteniana en una misión interestelar en la que se cruzan, cada vez a mayor velocidad, sistemas solares, galaxias y hasta cúmulos globulares.

Para entender el mínimo tamaño de un átomo, siempre me gustó la analogía de imaginar un átomo del tamaño de un estadio deportivo internacional. Los electrones se encuentran en la parte alta de las gradas; se ven tan pequeños como la cabeza de un alfiler. El núcleo del átomo está en el centro del campo y tiene el tamaño aproximado de un guisante. El átomo, pues, está casi vacío.

Plasmar los números de las cosas en estado puro es algo más complicado, pero una manera de visualizar un millón es usar un papel cuadriculado. Una hoja DIN-A4 de papel cuadriculado (con cuadraditos de 2 mm de lado) contiene unos 15.540 cuadraditos, por lo que con 65 hojas saldrán más de un millón. Otra opción es valernos del azúcar: un millón de granos de azúcar pesan alrededor de 700 gramos, mientras que un billón ascenderá a un poco más de tres cuartos de tonelada.

Una vez establecido esto, por ejemplo se puede imaginar más fácilmente las posibilidades que se tienen de acertar la combinación ganadora de una lotería primitiva estándar, que es de 1 entre 13.983.816 (un número que no podemos imaginar). Bien, mediante la analogía de la hoja cuadriculada, la cosa se aclara un poco más: acertar los seis números correctos de la lotería es como coger uno de los cuadraditos de 2 mm entre un fajo de 900 hojas.

En la escala del azúcar sería el equivalente a buscar un único grano negro entre 10 kg de azúcar.

Podéis seguir explorando números inimaginables en sendos artículos que ya escribí dedicados a los números muy, muy grandes y a los números muy, muy pequeños.

En Genciencia | Números muy, muy, muy grandes / Números muy, muy, muy pequeños

«Con cuatro parámetros puedo ajustar un elefante, y con cinco hacer que mueva la trompa» (Von Neumann)

¡Fácilmente!

Desde luego es que hay matemáticas definitivamente encantadoras: Cómo dibujar un elefante con cuatro números complejos. Una historia de John von Neumann, Enrico Fermi y Freeman Dyson recuperada ahora con una explicación completa por el siempre recomendable blog La ciencia de la mula Francis.

Proof: el blog de imágenes matemáticas

Proof es un precioso blog minimalista dedicado a imágenes matemáticas, detrás de las cuales se esconde toda una historia: una demostración, una teoría, cálculos complejos o el planteamiento de un problema. Cada imagen va acompañada de una pequeña descripción y los oportunos enlaces para indagar más en la belleza del mundo matemático.

Dos conjuntos de Julia fractales en la superficie de una esfera

Arnaud Chéritat del Instituto de Matemáticas de Toulouse tiene un montón de preciosas imágenes matemáticas en su web, incluyendo estos dos fractales del tipo conjuntos de Julia dibujados sobre la superficie de una esfera, como si se estuvieran besando, con un bello colorido.

§ Proof + Science is Beauty.

Matemáticos ofrecen una solución elegante a un problema evolutivo

Investigadores de la Universidad de British Columbia (UBC) han ofrecido un nuevo modelo matemático que busca desvelar un problema evolutivo clave – qué factores subyacen a la generación de diversidad biológica, tanto dentro como entre especies.

Los biólogos evolutivos han reconocido desde hace mucho que el surgimiento de rasgos extraños dentro de una población puede espolear la diversidad. Por ejemplo, ser uno de los pocos depredadores de pequeño tamaño en una población dominada por depredadores de gran tamaño puede tener sus ventajas – acceder a una abundancia de pequeñas presas – y la probabilidad de que el rasgo prospere en la población.

“Pero los modelos matemáticos existentes que incorporan estas ventajas del ‘tipo raro’ tienden a tener algunos serios obstáculos”, señala Michael Doebeli, investigador del Centro de Investigación de Biodiversidad de la UBC y profesor de los departamentos de Matemáticas y Zoología. “Dependen de rasgos aislados – como el tamaño del cuerpo – y predicen si la ventaja ofrecida por el rasgo será significativa para mantener grandes cantidades de diversidad”.

Por lo que Doebeli y el investigador asociado Iaroslav Ispolatov aplicaron un nuevo modelo al problema, el cual se esboza en el ejemplar de hoy de la revista Science.

Basándose en modelos de competición clásica para rasgos aislados, diseñaron una teoría matemática para evaluar el impacto evolutivo de múltiples rasgos a la vez, y encontraron que añadiendo esta capa de complejidad, disminuía considerablemente el umbral de mantenimiento de la diversidad y la evolución de nuevas especies.

“Cuando modelas un rasgo cada vez – en aislamiento – a menudo encuentras que las interacciones ecológicas no son lo bastante fuertes para dirigir la divergencia. Pero con muchos rasgos actuando a la vez, incluso las interacciones débiles pueden generar diversidad. Nuestra aproximación refleja la complejidad de la realidad más de cerca – si piensas en ello, todos los organismos vivos tiene al menos docenas, si no cientos, de rasgos ecológicamente relevantes”, dice Doebeli.

Matemáticamente, el fenómeno biológico se refleja en las propiedades fundamentales de eigenvalores de formas cuadráticas. La teoría ayudaría a explicar la extraordinaria cantidad de diversidad encontrada en muchos ecosistemas, por ejemplo, en el mundo microbiano de los océanos. De hecho, el terreno de pruebas inicial del modelo podría ser perfectamente las poblaciones microbianas.

“Sería interesante probar si a nivel genético, las rutas que controlan los distintos rasgos están reguladas en concierto para permitir la heredabilidad de la diversidad de rasgos a lo largo de múltiples cortes fenotípicos”.

Una Posible Explicación Para la Enigmática Proporción Aurea

12 de Febrero de 2010. Se cree que los egipcios la usaron para guiar la construcción de las pirámides, y que la arquitectura de la antigua Atenas se basó en ella. Y también se ha especulado sobre ella en diversas novelas de misterio.


"Ella" es la proporción áurea, una proporción geométrica que en varias teorías se ha señalado como la más agradable estéticamente para la vista humana, y que ha sido el origen de incontables misterios durante mucho tiempo. Ahora, un ingeniero de la Universidad Duke ha llegado a la conclusión de que es un camino para unificar la visión, el pensamiento y el movimiento bajo una sola ley de "ingeniería" de la naturaleza.

También conocida como la proporción divina, la proporción áurea describe un rectángulo con una longitud de aproximadamente una vez y media su ancho. Muchos artistas y arquitectos han realizado sus trabajos basándose en esta proporción. El Partenón en Atenas y la Mona Lisa de Leonardo da Vinci son ejemplos de la proporción áurea comúnmente citados.

Adrian Bejan, profesor de ingeniería mecánica en la Escuela Pratt de Ingeniería de la Universidad Duke, cree saber porqué la proporción áurea aparece en todas partes: Los ojos exploran una imagen más rápidamente cuando su forma concuerda con la de un rectángulo con la proporción áurea.

El "diseño" natural que conecta la visión y la cognición responde, según Bejan, a la teoría constructual. Concebida y publicada inicialmente por Bejan en 1996, esta teoría surge del principio básico de que los sistemas de flujo evolucionan para minimizar las imperfecciones (la energía gastada en la fricción u otras formas de resistencia) de modo tal que se pierda la menor cantidad posible de energía útil.
La teoría se aplica virtualmente a todos los movimientos. Por ejemplo, el flujo del tráfico, el enfriamiento de dispositivos electrónicos a pequeña escala, las corrientes de los ríos y las relaciones universales entre la masa corporal de los animales y su velocidad, así como la frecuencia y fuerza de sus pasos, aleteos u ondulaciones que propulsan sus cuerpos hacia adelante.

Bejan afirma que el mundo, ya sea el que aprecia un humano que mira una pintura o el que ve una gacela que escudriña el horizonte en una planicie, básicamente está orientado sobre la horizontal. Para la gacela, el peligro proviene principalmente de los lados o de atrás, no de arriba o de abajo, así que su campo de visión evolucionó para ir de un lado al otro. Bejan sostiene que conforme se desarrolló la visión, los animales se hicieron más "astutos" al ver mejor y moverse con más rapidez y seguridad.

Para Bejan, la visión y la cognición evolucionaron juntas y tienen el mismo "diseño" que la locomoción. La mayor eficiencia del flujo de información proveniente del mundo y conducido a través de los ojos hacia el cerebro se corresponde con la transmisión de esta información mediante la arquitectura ramificada de nervios y el cerebro.

Aunque la proporción áurea brindó una entrada conceptual en esta perspectiva de "diseño" de la naturaleza, Bejan ve algo incluso más amplio. Considera que la proporción áurea unifica la visión, la cognición y la locomoción de casi todos los animales terrestres.

Información adicional en:

• Scitech News

Fibonacci y proporción áurea

Nunca había en­ten­di­do del todo bien por qué cuan­to más avan­za­mos en la serie de Fi­bo­nac­ci, al di­vi­dir dos ele­men­tos con­se­cu­ti­vos, el re­sul­ta­do tien­de al nú­me­ro áureo. Mu­chas veces, este cu­rio­so re­sul­ta­do se pre­sen­ta como un mis­te­rio in­son­da­ble, una ex­tra­ña ca­sua­li­dad, cuan­do es tan fácil de ex­pli­car como esto:

Matemática, ¿ya estás ahí?

.

Anterior 1 de 2 Siguiente

Anterior 2 de 2 Siguiente

09.08.2009 | Según un estudio realizado por científicos argentinos, el cerebro tiene nociones innatas preexistentes a la cultura y a la enseñanza. Entre ellas destaca la matemática. Claro está que la instrucción hace que esa capacidad logre explotar y salir del rudimento.

Un grupo de científicos argentinos encabezados por Pablo Argibay, director del Instituto de Ciencias Básicas y Medicina Experimental del Hospital Italiano, explicó que hay ciencias básicas como la matemática que tienen un carácter innato en el conocimiento de las personas. Para ejemplificar, hay tribus que sin tener acceso a un tipo de aprendizaje del estilo convencional, logran realizar cálculos como una noción preexistente.
El especialista relató cómo es el desarrollo de estos estudios y además señaló cómo esto se relaciona con el análisis de algunas enfermedades ligadas a la mente. Además se refirió a otras investigaciones que buscan mejorar la calidad de vida de las personas mayores, ya que en poco tiempo más una de cada tres personas de más de 80 años sufrirá de Alzheimer.

N&P:- ¿Realmente todos de manera innata sabemos matemáticas?
P.A.:- Ya hay muchos estudios hechos por gente de Francia y en Estados Unidos que lo muestran no sólo en los adultos y los niños, sino también en los bebés y los monos, los primates del viejo mundo, primates avanzados parecidos al ser humano que tienen la capacidad de distinguir sin ningún tipo de enseñanza, cantidades al bulto. Sin contar, sin poder analizar superficies o volúmenes, pueden decir dónde hay más en un conjunto de puntos.

N&P:- ¿Qué sentido juega en esas operaciones? ¿La vista?
P.A.:- No sólo a través de la vista, sino también por el sonido o por el tacto se pueden hacer operaciones de ese tipo. ¿Cómo se parece un conjunto de puntos? ¿Se le saca ese otro bulto o se le agrega? Se logran distinguir con una certeza del 90% esas cantidades. En tribus donde no hay ningún tipo de concepción matemática ni enseñanza, que están despegadas de la cultura occidental, también son capaces de resolver problemas con conceptos matemáticos. Lo que un poco dirime la cuestión de si hay un innatismo, una mínima habilidad matemática que vemos que esos estudios describen.

N&P:- ¿Esto indicaría que hay una capacidad innata preexistente a aquello que hemos ido incorporando desde la cultura?
P.A.:- Sí. La discusión es, y más aquí en la Argentina, que tiene que haber un clásico de los clásicos, naturaleza versus cultura. Lo que este estudio muestra claramente es que es obvio que al ser objetos evolutivos venimos con un bagaje previo a la cultura. Nacemos con esa preparación de nuestro cerebro para algo, pero que una enseñanza formal y bien dirigida, más en el caso de las matemáticas, mejora notablemente sus habilidades. Por lo tanto no hay tal discrepancia entre naturaleza y cultura sino que es una interacción permanente. Uno viene obviamente con un cerebro que está preparado para el habla, para el cálculo, para varias cosas, pero sin la cultura quedaría como rudimento para esas operaciones.

N&P:- En ese aspecto, ¿la cultura y la educación son las que lo van formando?
P.A.:- La cultura y la educación lo mejoran notoriamente. Y el interés final es ver si se puede aplicar esto en aquellas personas que tienen algún tipo de discapacidad cognitiva, como pueden ser personas muy mayores o en el caso de niños que tienen habilidades especiales como los autistas. Si vio la película “Rainman”, se caen fósforos, y el personaje puede decir la cantidad exacta sin haber hecho ningún tipo de cálculo.

N&P:- ¿Son habilidades que tiene la mente, pero que en la conducta de las personas no autistas no son explicitadas?
P.A.:- Lo que pasa es que estas habilidades especiales están muy lejos de la comprensión de cualquier persona que no tenga el problema. Eso escapa a la velocidad de cálculo; el procesamiento que ese cerebro hace es otro y es muy parecido a ese procesamiento inicial que se trae y que luego es cambiado. Parecería que muchas veces esos niños autistas -estamos hablando de niños autistas especiales con capacidades especiales- quedan bloqueados en alguna especialidad. Hay niños que tienen esas habilidades, pero luego, por ejemplo, carecen de la posibilidad de atarse los cordones de los zapatos. Es decir que evidentemente es una capacidad innata, algo que ha quedado bloqueado que no permite desarrollar estas habilidades, pero que de alguna manera aparecería un poco de la mano de este tipo de fenómenos que estamos estudiando muy inicialmente.

Investigaciones

N&P:- ¿Qué caminos indican este tipo de trabajos en la búsqueda de comprender el cerebro?
P.A.:- El objetivo básico es entender por entender qué es lo que busca la ciencia básica y después habría dos objetivos muy pragmáticos. Uno sería entender las enfermedades mentales. No nos olvidemos que las enfermedades degenerativas del cerebro -en muy pocos años una de tres personas mayores de 80 años va a tener Alzheimer- son un tipo de enfermedad que está aumentando porque se ha prolongado la vida, se han prolongado los factores nutricionales y un sinnúmero de cuestiones que tienen alta gravitación en el tema. Por eso es fundamental empezar a entender cómo se regenera, cómo se comporta, cómo se cablea, de qué manera lo podemos preservar.

N&P:- ¿Cuál sería el otro objetivo que se han impuesto?
P.A.:- Bueno, lo otro tiene un interés que raya un poquito con la ciencia ficción, pero es tratar de aprender de qué manera procesa el cerebro para construir algún tipo de prótesis o máquinas que simplemente sean capaces de hacer ese tipo de procesamiento, aprender del funcionamiento cerebral para construir elementos que sean capaces de funcionar como funciona el cerebro. No serían robots, serían sistemas neuromórficos; son sistemas muchísimo más avanzados. El objetivo de nuestro instituto es algún día crear prótesis que permitan a una persona que tenga un área afectada “puentear”, saltar ese déficit con un circuito que funcione de una manera similar a como funciona el cerebro. Pero es para dentro de muchísimos años, son estudios que están recién en su fase inicial.

N&P:- Un tema en el que se ha avanzado notablemente son los mapeos cerebrales, ¿verdad?
P.A.:- Sí, a lo largo de la vida, a pesar de todo lo que se pierde a medida que se avanza, el cerebro tiene una capacidad asombrosa llamada neuroplasticidad, que es la habilidad de ir reforzando algunos sectores y en el caso del déficit ir cubriéndolo con otro tipo de sector. Es decir, es una habilidad que se tiene y que en los niños es inmensa. Se pierden áreas enteras y son recuperadas por otras áreas. Eso es la neuroplasticidad, y cada vez es más explotada en la rehabilitación de los accidentes cerebrovasculares y otro tipo de lesiones. Pero es una de las características que lo hace maravilloso, que es esa capacidad de recableado que tiene, y por tanto la posibilidad de reinstaurar algunas funciones.