La mecánica cuántica explica el rango completo de curvas de fuerza-relajación que producen los músculos, de acuerdo con un nuevo estudio.
No hace mucho tiempo los biólogos habrían jurado sin pensárselo que su disciplina nunca se vería contaminada por los extraños efectos de la mecánica cuántica. Hoy, la biología cuántica es una disciplina emergente en muchos laboratorios de todo el mundo y sólo los más osados (o estúpidos) debaten contra la idea de que los efectos cuánticos desempeñan un importante papel en el funcionamiento de las moléculas biológicas, en células completas, e incluso en el cerebro.
Hoy, los músculos se añaden a esta lista. Tieyan Si del Instituto Max Planck para Sistemas Complejos en Dresden, Alemania, ha creado un modelo cuántico del comportamiento de un músculo. Su idea es que la miosina, el motor molecular indispensable para la contracción muscular, es, básicamente, un objeto cuántico y que su comportamiento se describe mediante la mecánica cuántica.
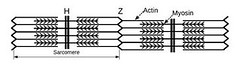
La parte importante de la fibra muscular consta de actina, que puede imaginarse como una cuerda, y la miosina, que es un motor molecular que funciona como un equipo de sogatira. La estimulación eléctrica pone en acción a los equipos, tirando de las sogas frenéticamente y provocando que se contraiga el músculo. La fuerza real que produce un músculo es el resultado de muchos motores de miosina tirando y relajándose, aunque no necesariamente en orden.
El reto para los teóricos es descubrir cómo estos motores moleculares generan la fuerza y las curvas de relajación que tienen lugar en los músculos reales. Esto está bien estudiado en sistemas tan diversos como el músculo del corazón mamífero y las alas de los insectos, y los biomecánicos saben desde hace tiempo que distintos tipos de músculos y distintas acciones musculares, producen distintas curvas de fuerza. Por ejemplo, las contracciones que se liberan rápidamente tienen una señal de fuerza distinta a las que se liberan lentamente. Explicar esto con una única teoría clásica no es fácil.
La aproximación de Si es simplemente suponer que cada motor de miosina es un objeto cuántico que puede tomar dos formas y que el cambio entre estas formas provoca la contracción. En otras palabras, tiene dos estados. (También estudia un sistema en el que la miosina tiene tres estados). La miosina cambia de un estado a otro absorbiendo energía y relajándose emitiéndola, y el efecto combinado todos los cambios determina el comportamiento de la fibra.
Entonces, una fibra muscular es, simplemente, una cadena de estos objetos cuánticos, para la cual es posible derivar matemáticamente el objeto conocido como Hamiltoniano, que describe su comportamiento. La cuestión que aborda Si es a qué tipo de curva fuerza-relajación lleva este Hamiltoniano.
Su respuesta es que “este sistema Hamiltoniano cuántico nos da la relación clásica fuerza-velocidad no sólo para una liberación rápida, sino también para una lenta y estados inestables”.
Demuestra que el sistema de dos niveles modela con precisión el comportamiento del músculo del corazón mientras que el de tres niveles el comportamiento del músculo de vuelo de un insecto.
Lo que Si no explica con claridad son los fallos de los modelos convencionales del comportamiento muscular, y por qué la aproximación cuántica es mejor. Tampoco hace Si ninguna predicción sobre el comportamiento de un músculo que no pueda hacer un modelo clásico.
No obstante, este es un impresionante primer paso hacia la descripción cuántica del comportamiento muscular. Y, como señala Si, hay mucho más trabajo por hacer para comprender el interfaz entre la cadena cuántica y las señales que las disparan, tales como señales eléctricas a lo largo de los nervios y el flujo de iones a través de las membranas que éstas disparan.
Artículo de Referencia: arxiv.org/abs/1004.3120: One Dimensional Chain Of Quantum Coherent Molecule Motors As A Model For Muscle Fibre
Fecha Original: 21 de abril de 2010
Enlace Original
No hay comentarios:
Publicar un comentario